This post discusses an older paper that shows how a clever idea (butterfly factorizations) can be learned in a typical deep-learning pipeline. It concludes with some conjecture how these fast algorithms can be applied to other slow, data-intensive algorithms: attention.
[mathjax]
Learning fast algorithms for linear transforms with butterfly factorizations. Tri Dao (author of FlashAttention), Albert Gu , Matthew Eichhorn, Atri Rudra , and Christopher Ré
I’m surprised this paper isn’t more cited – it really is quite clever & well written.
Idea: useful linear transformations (DFT/FFT, discrete cosine/sine transform, Hadamard) can be expressed recursively as the product of “butterfly” weight matrices (e.g. elements are powers of $latex e^{i 2 pi / N}$ with the FFT) and permutation matrices (a bit-reversal permutation with the FFT).
Both matrices can be learned from input-output pairs; the resulting algorithm is $latex O(N log N)$ vs $latex O(N^2)$, with $latex 4N + 3log_2 N$ parameters vs. $latex O(N^2), N^2$ parameters for a full-rank matrix.
In the figure below, each one of the red pixels corresponds to a free real or complex parameter; the second block is replicated twice, the third 4x, the last 8x (= weight sharing) so that $latex 2N+N+N/2 … = 4N $
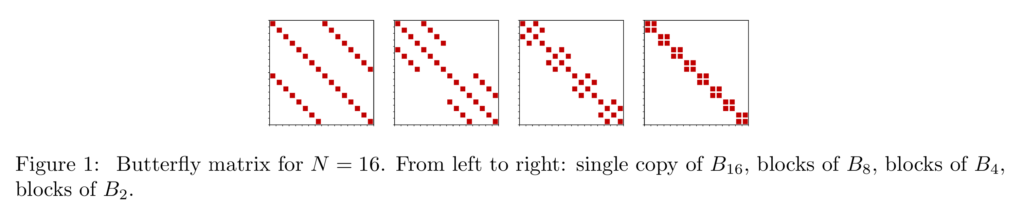
These 4N parameters are not tied, which generalizes the transforms.
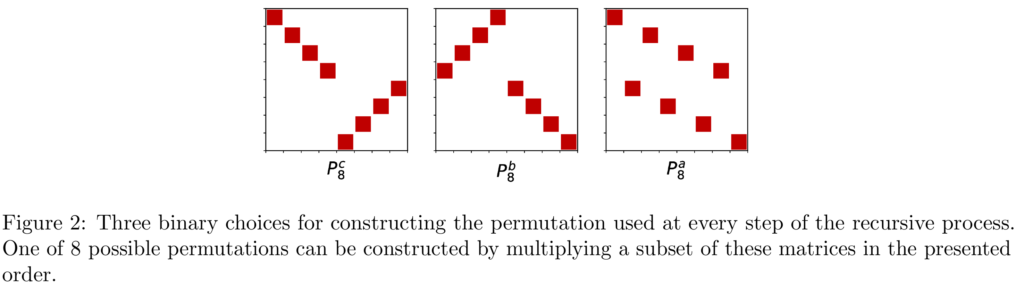
The permutation matrix is in turn learned via a softmax selector over 8 preset permutations, which are sufficient to express the common fast transforms. (This can be encoded as 3 binary bits (done here) or as an 8-way softmax (done in follow-up work)
Since you can represent convolution as pointwise multiplication in Fourier space, by composing two butterfly-permutation pairs you can do convolution. When applied to CIFAR-10, this form shows 56x parameter compression with an increase in accuracy relative to a full-rank matrix.
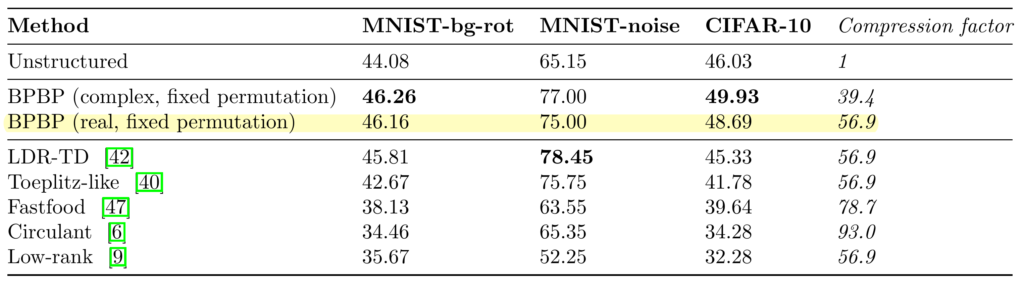
Caveat: they do not show stacking more than one layer, and hence while the compression is excellent, the absolute performance is mediocre (modern vision transformers yield > 95% accuracy).
Though the associated git repo is bitrotted (does not compile with CUDA 12.1), I really like the concept:
Force a recursive structure to encourage representations that are more invariant (or equivariant) than the original. (This can be achieved also with full-rank, non-factorized matrices — albeit with quadratically more data!).
This idea of invariance is explicitly encoded in the butterfly matrices: all $latex B_2$ are identical, independent of location, and are combined in a uniform manner based on $latex B_4$. Yet this is not position-invariance due to the permutation matrices, which instead say that the data at alternating indices should be treated the same, times a (complex) scaling factor. In the case of DFT/FFT, this encapsulates the observation that “things tend to oscillate, and do so at different timescales”.
Can this sort of logic be applied to attention, another famous (and limiting) $latex O(N^2)$ algorithm? Many many people have tried, and there are indeed low-rank approximations to the attention matrix (like the Nystromformer), yet in practice it seems most Transformers operate with a full attention matrix = full DAG of token dependencies. Because tokens are not sampled uniformly (sentences tend to be heterogeneous), and meaning is query-dependent and derives from this heterogeneous context, a naive $latex O(N log N)$ application of sparse butterfly matrices would not work.
Yet: by construction the attention matrix is $latex \sim N$ -sparse (due to the softmax), and indeed much real-world data (like a program AST) is hierarchically & log structured, suggesting that compression in time or space is possible. Caching is already commonly used, of course, but it seems very likely that an asymptotic $latex O(N log N)$ implementation of attention is possible with the correct treatment – I suspect that the $latex log N$ term will be via an expansion in time = variable compute = amortized search or dynamic programming.