From Pairwise to Higher Order Tensor Operations on GPUs

Pairwise primitives are a primary operational pattern in deep learning. They take two inputs and fuse them into a single output. Matrix multiplication, dot product, and element-wise or Hadamard product are all examples of this. In transformers, self-attention computes relationships between pairs of tokens. Similarly, gating mechanisms such as Gated Linear Units (GLUs) combine two signals via component-wise multiplication – one vector gates or modulates another.

These are extremely useful for capturing complex relationships in high dimensional space. For example, self-attention can capture long-range dependencies in input sequences, and gating units stabilize and enhance representational power of neural network learning. However, pairwise primitives are by definition limited to two inputs, treating interactions as linear or bilinear combinations. To capture higher-order dependencies between three or more inputs, networks must compose sequences of pairwise operations to approximate n-way linkages. This requires coordinating intermediate computation, making the process potentially sample inefficient.

However, if we could raise the arity of the core primitives from two (pairwise), to three or more, we may be able to encode multi-input relations in fewer steps. In other words, raising the interaction order of the model’s basic operation can reduce or hide the complexity of representing certain functions.

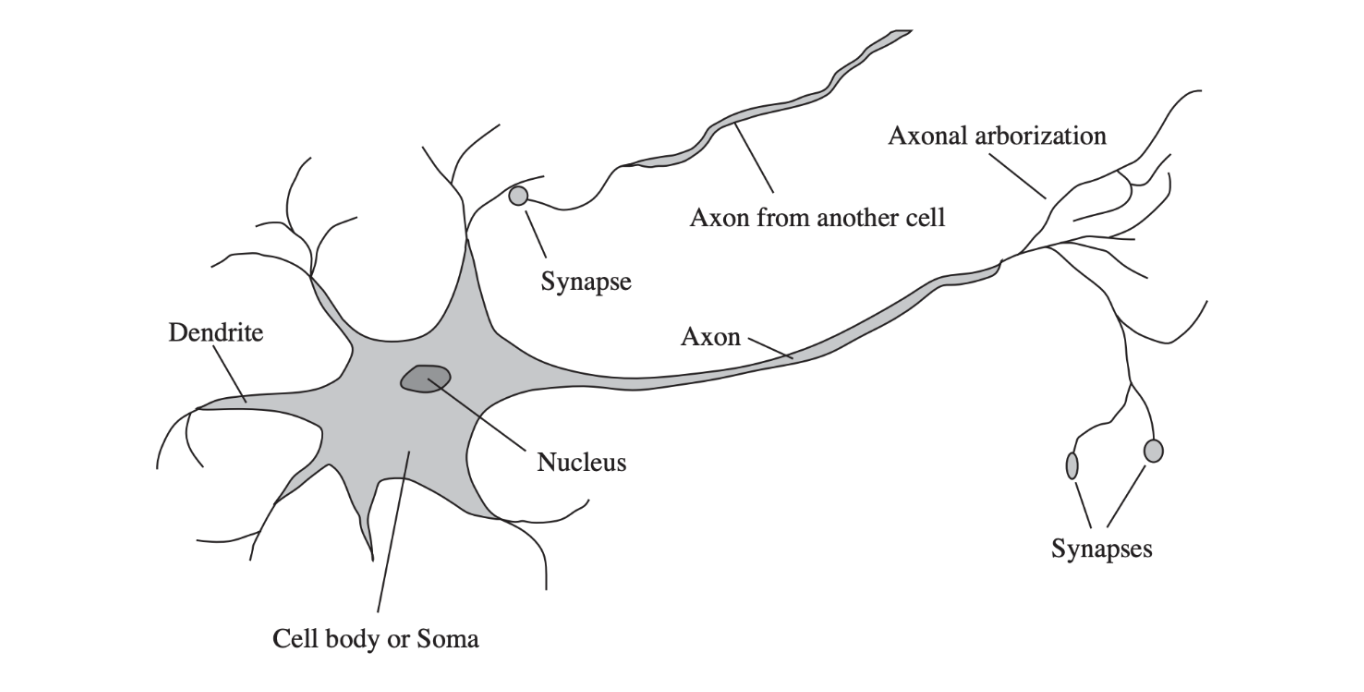
Dendrites in biological neurons demonstrate this already. Dendritic branches receive groups of input from other neurons at specialized junctions called synapses. Summing these inputs would yield a plain \(\sum \). But dendrites contain many non-linear mechanisms to process and integrate synaptic signals before passing it to the cell body and later down the axon [2, 3]. Dendrites and synapses act like sub-circuits that multiply or gate inputs, so one input can amplify, suppress, or rewire how two other inputs combine [4, 5] – this effect is particuarly apparent with spine-neck inhibition, for example. These are multiplicative or conditional interactions (for eg. the effect of input A depends on B and C), meaning they represent higher-order linkages and dependencies. As such, dendrites in neurons directly support higher-arity primitives, meaning one biological neuron can natively represent functions that an artificial neural network would approximate only by combining many pairwise units across layers [6].

Native support for n-way dependencies also hypothetically provides increased support for compositionality, a core component of intelligence [1]. Compositionality is necessary for out-of-distribution generalization as it enables a model to combine known concepts to adapt to novel environments [7]. Composition depends on binding parts so they can be reused and recombined. Multiplicative, higher-order interactions (e.g., triadic terms) support binding since they create units that depend jointly on multiple factors and can be composed again downstream [6].

Modern LLMs famously suffer in this domain, specifically from something called the “compositionality gap” i.e. the ratio between how often an LLM can solve simple problems vs how often it can solve composite problems [8]. It is no coincidence that they are built using pairwise primitives, and any support for compositionality is external to the model in the form of laborious prompting techniques and fine-tuning from human / automated supervised data.

1 Tensor Contractions

Pairwise primitives are a special case of a broader mathematical framework: tensor contractions. A tensor contraction takes two or more tensors and contracts them by summing over pairs of products of indices. Specifically, it zips two indices together by taking an element-wise product, and then summing over the zipped index. This reduces the rank of the original pair of tensors by 2. Matrix multiplication is a type of dyadic tensor contraction. While matrix multiplication contracts over one shared dimension between two tensors, tensor contractions can operate on arbitrarily many tensors with complex dimension-sharing patterns, enabling multivariate primitives.

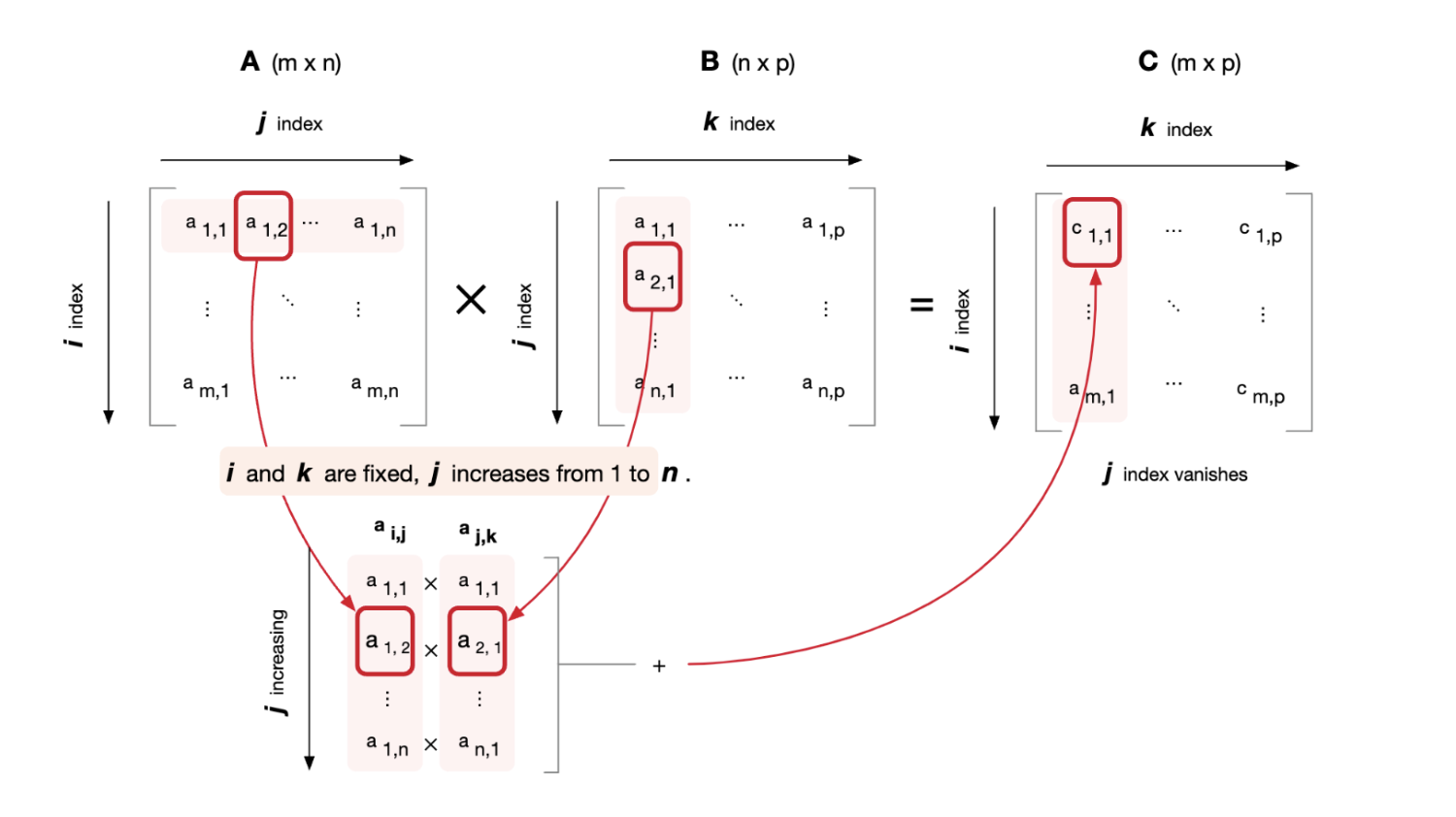
However, implementing tensor contractions results in fundamental hardware constraints that become apparent even with simple pairwise operations. A direct matrix multiplication of two \(n \times d\) and \(d \times n\) blocks produces an \(n\times n\) object, which is quadratic in compute and storage. While compute time can be parallelized across thousands of GPU threads/cores, space still scales as \(O(n^2)\) and is much more complicated to configure on GPUs.

Standard self-attention, for example, exhibits quadratic scaling.

Here, Q, K and V are all shaped (seq_len, d), which means that doing \((Q \cdot K^T)\) requires us to hold a \(\text {seq\_len} \times \text {seq\_len}\) matrix in memory so that we can Softmax over its rows.

If seq_len = n and we are using float16 precision, then we get:

• n = 16,384: 16k \(\times \) 16k \(\times \) 2 bytes = 0.5 GB (Manageable)
• n = 65,536: 65k \(\times \) 65k \(\times \) 2 bytes = 8.6 GB (Significant portion of GPU memory)
• n = 150,000: 150k \(\times \) 150k \(\times \) 2 bytes \(\approx \) 45 GB (Consumes most of a top-tier GPU for just one attention score)

This is just for a single attention head in a single layer – transformer models typically use multiple heads and dozens of layers. The memory requirements quickly become prohibitive for long sequences. The situation becomes dramatically worse when considering higher-order operations. For a triadic \(n \times n \times n\) tensor with n = 16,384, the memory requirement explodes to 8 TiB – over 100x larger than the largest available GPU memory. These are non-trivial memory challenges that require non-trivial solutions.

Running experiments with higher order operations is something we have had to reckon with as we build a machine learning strange loop. In doing so, we realized that we need to write custom CUDA kernels and use special tricks to extract the maximum juice from GPUs.

Naturally, we used the flash attention papers as inspiration. Ever since self-attention, researchers have been experimenting with variations (Linformer, Performer, Reformer, Longformer) to achieve sub-quadratic memory & compute scaling. However, most of these suggestions use sparse or approximate methods instead of exact attention scores, and may struggle with performance in practice. Flash attention was a step change over these methods because it yields exact attention scores, while slashing memory usage down from quadratic to linear complexity [10]. Since its release in 2022, it has become the de facto standard kernel for LLM training and inference.

2 GPU Memory Hierarchy

Flash attention achieved linear memory usage by never materializing the full \(n\times n\) score matrix and using the memory hierarchy within GPUs to achieve performance gains. In order to understand their techniques, it is necessary to know how memory works in a GPU.

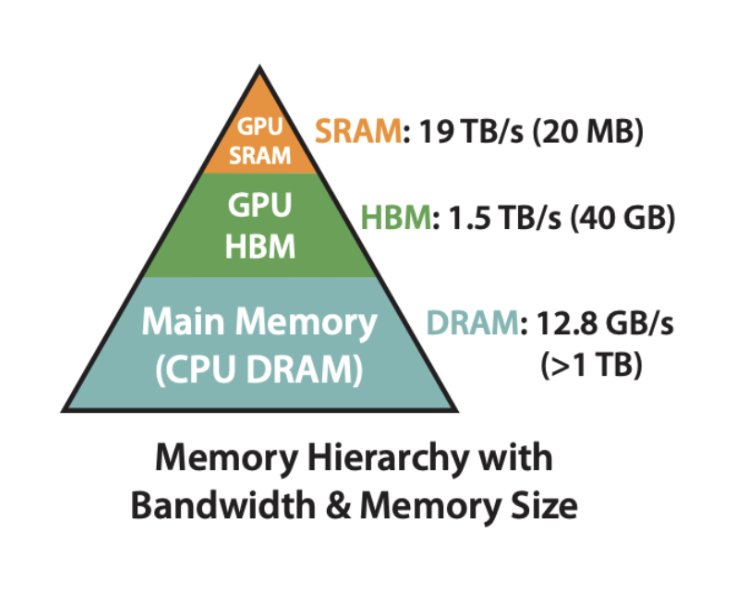
GPUs have a “steep” memory pyramid. HBM lives off-chip, making it the slowest form of memory storage, since data has to travel physically on and off chip for memory read/writes. It is also typically the largest memory storage. On kernel launch, input tensors are loaded into HBM. L2 cache is faster – it’s on the GPU die – but is much smaller, and still has limited bandwidth. Every memory request that cannot be satisfied within the shared multiprocessor (SM) must pass through L2 on its way to HBM. On the other hand, registers, shared memory, and the L1 cache all live within the SM. These are far smaller than HBM or cache, but much faster to access – one clock cycle for registers.

Shared memory is orders of magnitude faster and smaller than HBM, but must be managed explicitly by the programmer. All threads in a block can cooperatively read and write to it. L1 cache that sits alongside its shared memory. Depending on the GPU architecture and configuration, part of its Static RAM is exposed as shared memory (explicitly managed by the programmer), and the rest is used as L1 cache (automatically managed by hardware). Together they provide a fast, on-chip buffer close to the cores.

Lastly, registers are the smallest and fastest type of memory storage. Every thread gets its own private registers (unlike shared memory, which is shared between threads in a block), and all arithmetic instructions read and write on registers by default (except for the new tensor ops). If a kernel needs more registers than are available on thread, the compiler will “spill” values into local memory, which actually lives in HBM and is orders of magnitude slower.

FlashAttention exploits this memory hierarchy using three techniques:

2.1 Tiling

Instead of keeping Q, K and V in HBM, FlashAttention loads smaller tiles or sections of data from HBM into shared memory, and works on each set of tiles separately [11, 12].

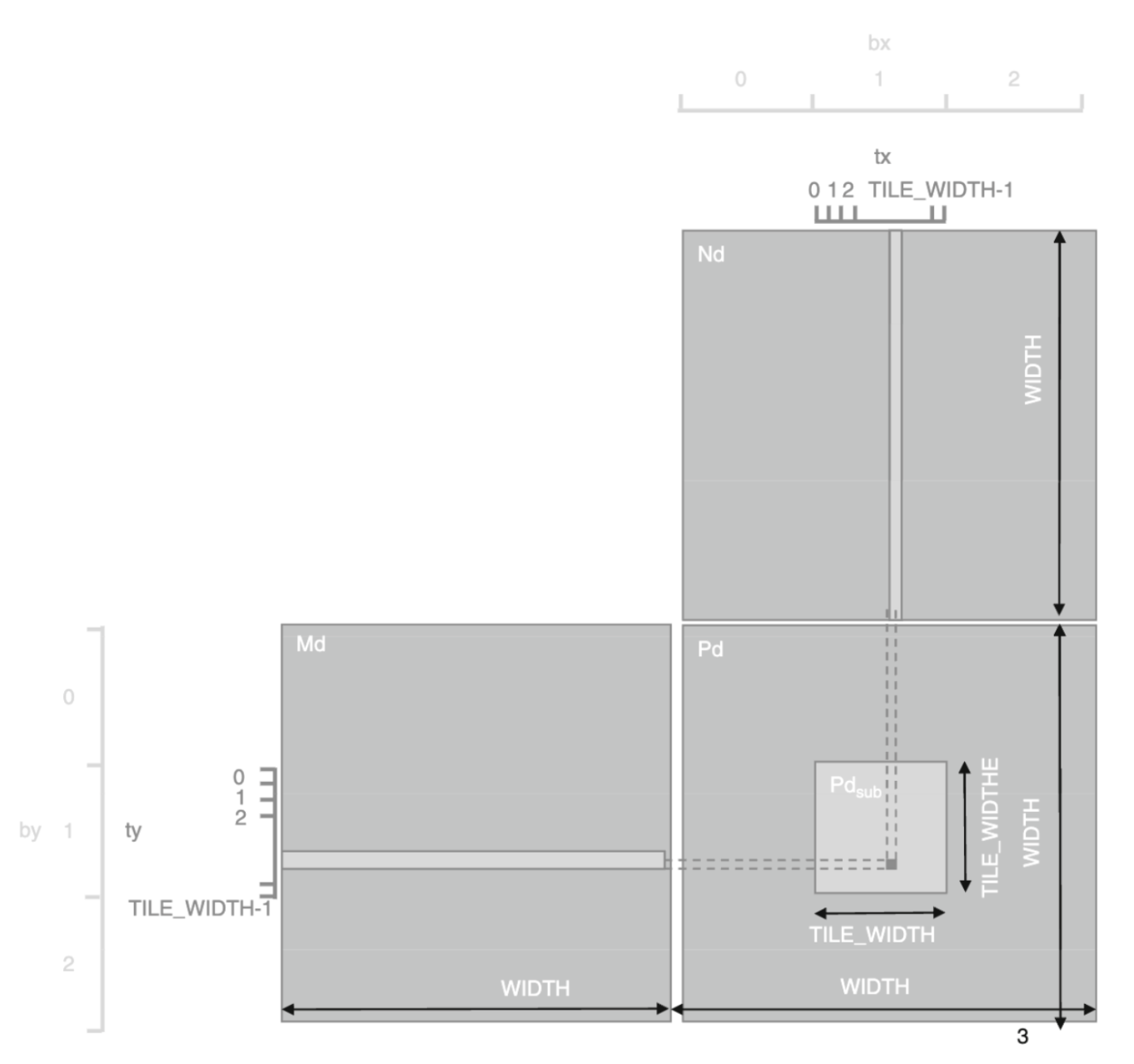
2.2 Online Softmax

However, there is shared dependency across tiles – the Softmax function has a normalization term in the denominator.

Notation: \(i\) = output row, \(t\) = tile index, \(s_{i,j}^{(t)}\) = scores in tile \(t\), \(v_j\) = value vector, \(m_i^{(t)}\) = running max, \(\ell _i^{(t)}\) = running denominator, \(o_i^{(t)}\) = running normalized output.

Naïvely, this requires holding the entire score matrix in memory so that each row can be exponentiated, summed, and divided elementwise. With tiling, we instead accumulate the needed quantities across tiles for each row \(i\) (let \(t\) index tiles):

Initialize \(m_i^{(0)}=-\infty ,\ \ell _i^{(0)}=0,\ o_i^{(0)}=0\). The factor \(e^{\,m_i^{(t-1)}-m_i^{(t)}}\) rescales prior accumulators when the running max increases. After the final tile \(T\), the normalized output is \(o_i = o_i^{(T)}\). In FlashAttention, these updates let us compute the exact result (up to floating point precision & rounding) without storing the full \(n\times n\) matrix.

2.3 Kernel Fusion

A naïve implementation of attention might launch separate kernels for score computation, softmax normalization, applying dropout, and multiplying by V. Each of those launches would write intermediate results back to HBM, only to reload them in the next step. This creates excess off-chip traffic. FlashAttention avoids that by fusing all of these operations into a single kernel. The scores are computed, normalized with the online softmax, and immediately used to weight V, all while the data stays on-chip in registers and shared memory. No intermediate results are ever written to global memory. This reduces both memory bandwidth pressure and kernel launch overhead, making the computation not just memory-efficient but also much faster in practice.

3 Generalizing to Higher Order Tensor Operations

For our kernels, we needed to work with 5-dimensional tensors without running into OOM errors. After peeling off the axes that are embarrassingly parallel (batch, heads, sometimes blocks of channels), we are left with a triadic tensor contraction. Each thread block owns a single output vector and streams over the remaining two axes in tiles. For each tile, a small block of the source data (and their value tensors) is loaded into shared memory alongside the output vector being updated. The block computes all pairwise scores within that tile and immediately folds them into the output while the data is still on-chip. Once the tile is consumed, it’s discarded and the kernel moves on to the next. This way, we never allocate a full 5D matrix. At any point, the active working set is just one compact tile plus the output vector in registers and shared memory.

Normalization is handled in the same streaming fashion. Instead of storing the full grid of scores to compute a global softmax, each tile contributes local statistics (max and sum of exponentials) that are reduced cooperatively in shared memory. Across tiles, the kernel keeps a running max, a running normalizer, and a partially accumulated output. When a new tile is processed, its contributions are rescaled into the same reference frame and merged in. By the end of the loop, the output is already normalized and complete.

All of this happens inside a single fused kernel for the most part. There are functions in the contractions that require multiple tiers of normalization, in which case we might use a mutli-kernel strategy where preliminary kernels only compute the running statistics needed for normalization terms.

We adapted these strategies for our kernels, and ended up bringing memory usage down from cubic to linear complexity. This allowed us to work with triadic tensor contractions and higher-order primitives without materializing the full tensor in memory.

A future post will describe in more detail the exact operations in the higher order contractions. We are actively testing and developing both the kernels and the models they are part of, so stay tuned!

References