To make a (ML) strange loop

1 Introduction

A key component of science is model induction – the translation of observation into models. In an analogy¹¹ Which can be formalized, to some degree – see [1]. to statistical mechanics & thermodynamics, one can think of this process as ‘pumping computational entropy’ – moving data (entropy of relations, as opposed to entropy of points) from a static repository into a computational or operational form. Such a ‘pump’ can also be run between different computational repositories, for translation, re-representation, compression, or other forms of optimization.

This idea of pumping computational entropy is²² In my opinon! a more well-defined, principled, actionable, and moral of a goal for machine learning than “AGI”. Much the same way that industrial revolutions of the past have pumped / transformed and moved physical entropy (or enthalpy), with machine learning we now pump information. Science itself is such a pump, one which uses models to seed and select (potentially costly) observations, which are then compressed into models. The resulting understanding – computational models – can be used to advance technology, fix ourselves or our world, or critically work as computational pumps, translators, or compressors: modelling model induction = building pumps.

This gets to another other salient fact about science (and mathematics): they are strange loops – what Douglas Hofstadter defined as any system that self-referentially acts upon itself. In his book I am a strange loop, he gives a few examples of, most notably Godel’s incompleteness theorem and our conscious selves. Science and mathematics also act upon themselves, self-modify, self-reference, and re-exploit computational and representational motifs at all levels for compression & understanding; their ability to self-reference is instrumental for inducing new models & pumps in themselves – this is what science is! Modelling model induction implies a strange loop, too.

The goal of Springtail is to build a machine-learning strange loop.

2 Why

The need for such a system became clear during the past \(\sim \)1.5 years of research undertaken on small mechanistic reasoning models³³ Note: strange loops in machine learning is not a new idea by any measure – Yann LeCun mentioned it years ago, see this youtube talk. Our models focus on solving constraint-satisfaction problems, which can be small enough for 1-minute training experiments, but expansive to large and hard real-world problems (e.g. placement and routing for PCB or IC/ASIC design).⁴⁴ Sudoku, the most familiar of CSPs, is none-the-less NP-complete when expanded beyond the 9 x 9 grid; indeed, the hardest sudokus require multiple levels of graph-coloring & chained inference to directly solve. Part of the work focused on representational efficiency and out-of-data generalization, for which we developed a new form of transformer attention. Other work, undertaken by Justin Jung, focused on data efficiency; he showed that diffusion dramatically decreases the data requirements of transformers.

2.1 Data efficiency

In the many experiments on increasingly hard problems, it was always us that closed the final informational loop, always the humans at the keyboards that injected or changed the models or algorithms to improve the fit, compression, or pumping. This is by necessity: ML models can readily learn heuristics from troves of data, but on symbolic & model-induction tasks (like changing model structure), even the largest models struggle [2]. Frustratingly, the algorithms and meta-algorithms for accomplishing sample-efficient learning are the same as the algorithms being learned by the underlying models! Namely: search, counterfactual reasoning, backtracking, basic set operations, modus tollens, modus ponens, law of the excluded middle, and other algorithms for (Bayesian) induction / deduction.

Collectively, these human-invented rules are far more data and compute efficient in their particular domains⁵⁵ Usually discrete spaces, as opposed to the high-dimensional and undercontrained spaces often found in ML. than SGD and its cousins operating in high-dimensional deep-learning space. SGD has the strong advantage of generality, statistical robustness, and in some cases near-optimal efficiency [3], but it defaults to memorizing or one-step approximation [4], learning heuristics [5]; and only later (with much more data, algorithmic changes like diffusion, or researcher intervention) will it learn parsimonious functional forms [6]. These forms are computationally compressed but only somewhat generalize out-of-data, as desired; they also tend to be black box & inscrutable, so are hard to invalidate, as required for science.

Why are we always using a slow learning algorithms, even after learning fast inference rules? The answer, of course, is that normal machine-learning workflow separates the model (some form of parameterized neural network) and the optimizer/pump (a variant of SGD).

Removing the delineation requires a strange loop⁶⁶ C.f. Jacques Pitrat’s pioneering work, which used a hierarchy of workers – managers – supervisors to close successively larger and larger feedback loops [7].

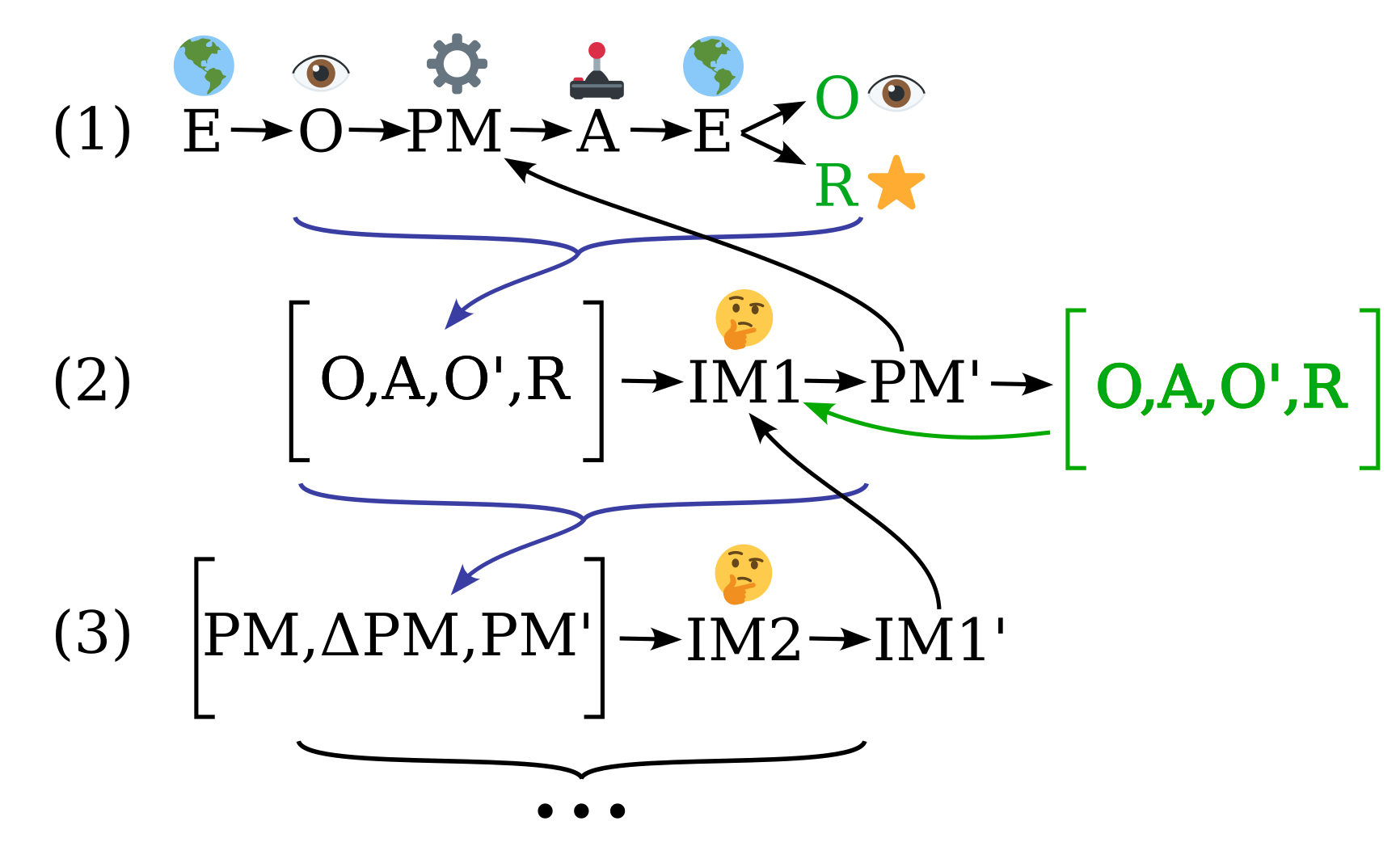
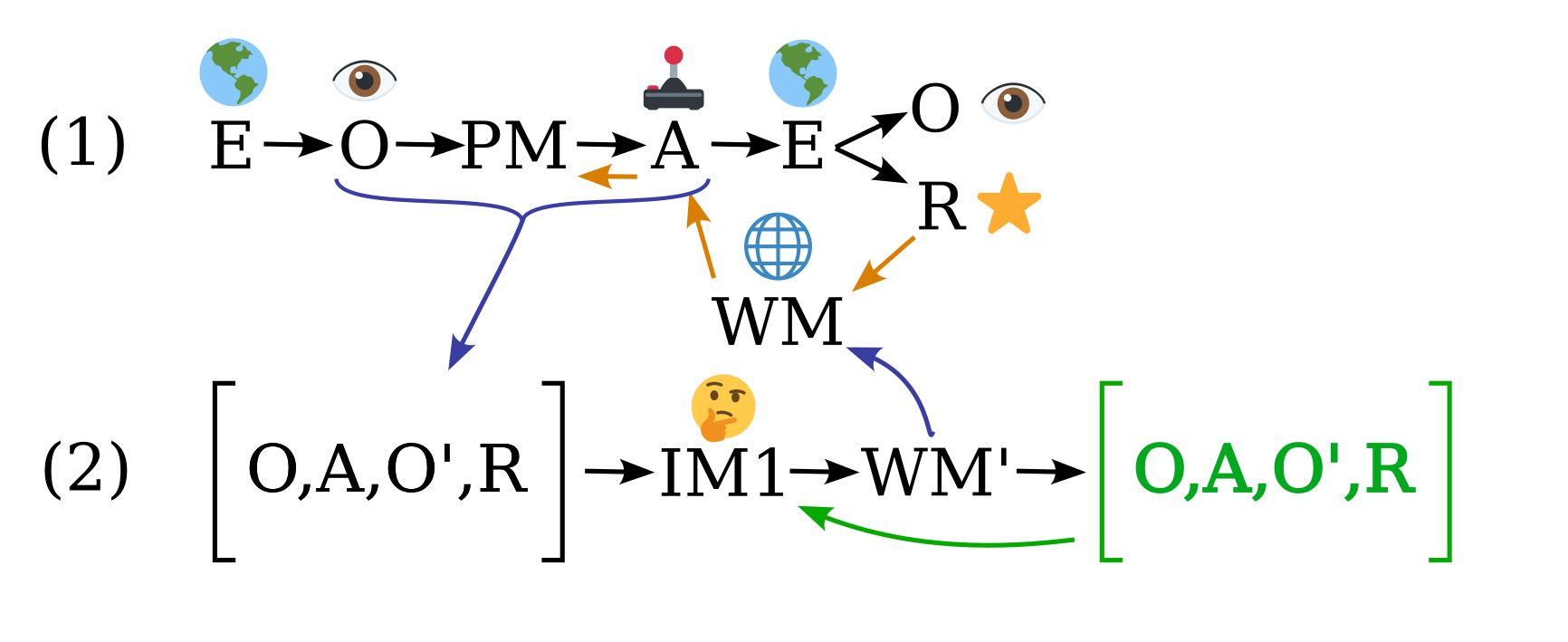
See Figures 1 and 2 for illustrations how strange loops can collapse depth- and breadth-wise open-ended modelling problems.

2.2 Aren’t we there already?

A critical eye will note that modern ‘reasoning’ LLMs already evince a strange loop – they generate and ingest their own tokens, triggering rounds of perception and generation that can solve hard problems⁷⁷ For example, OpenAI o3, which solved many ARC challenge puzzles – albeit after generating millions of tokens. This is a fair criticism; I cannot discount the tremendous progress & advances made over the past few years. Yet if the ultimate pump is some form of SGD, building novel functional structures, as required for open-ended compression or scientific model induction, will require boil-the-ocean levels of compute and data [8] (e.g. from oracles, as DeepSeek is doing, and was likely required to train o3 to solve the ARC challenge).

Beyond environmental and capital cost of the current approach, there are real algorithmic reasons for insisting that it won’t get to arbitrary computational entropy pumping (the principled version of “AGI”) or even discovery⁸⁸ Yann leCun – Why Can’t AI make it’s own discoveries. In the weaker token-only strange loop reasoning, some pumping can be done by rules of inference, selection, and perceptual modules/functions learned by the LLM from human examples⁹⁹ A dominant hypothesis is that reinforcement learning on LLMs (RLHF, RLVR) does not induce new structure in models, rather it re-weights structure already there. This is supported by observed reduction in diversity and ’catastrophic forgetting’ following fine tuning [9]., but the final pump is always some form of SGD, with its generality but undesirable limitations mentioned above. Put another way: the complexity of the pump does not directly increase with time, limiting the ability to go against arbitrarily-high entropic barriers. To return to the industrial revolution analogy, we need our tools to be able to lift heavier loads than us.

3 How

There are at least three technical innovations required to create a strange loop in a machine learning model.

3.1

Primary is the need for what Douglas Hofstadter calls ‘symbols pushing around symbols’ – more concretely, the ability for symbols (tokens) to modify the content and linkages between other tokens, irrespective of their contents. Vanilla transformers can only do this by emitting and re-ingesting tokens, as the graph of operations in the feed-forward architecture is effectively limited to ‘gather’ operations¹⁰¹⁰ That same critical eye here will note that even vanilla transformers are Turing complete, given infinite tokens, and either unlimited layers[10] or unlimited latent dimension (hence unbounded compute). This is true, but we are seeking something more general & efficient. Higher-order operations are possible in low-order systems; you can design a binary adder in Conway’s Game of Life, but it requires polynomial state and compute. Increasing the fundamental arity of the model’s operations is essential for making “symbols pushing around symbols” work in bounded space. . To address this we are actively developing a novel attention module for PyTorch that allows for symbols to create or destroy connections between other tokens We have a prototype in PyTorch and C++, and are finishing the CUDA implementation.

3.2

Second is enabling truly ‘relocatable’ and callable functional modules: (A) the algorithms learned by the model & instantiated into the transformer’s heads need to by default generalize out-of-domain (OOD), and (B) modules work flexibly based on the underlying symbolic schema. This is a direct consequence of the need to learn rules of inference, which act as higher-level functions from computer science.

• (A) We’ve begun tackling the OOD problem by using the L1 transformer to encode linear spaces with reals, rather than Fourier features [6]; this allows for transparent encoding of extensible spaces, easier “pointer access” for computed addressing (which otherwise requires trigonometric function calculation, e.g. with RoPE / Fourier features). Due to the intrinsically variable scaling of linear spaces, this makes training harder, though there are precedents for stable normalization [11] ¹¹¹¹ Softmax has the strong benefit in that its Jacobian has a bound norm, which means that attention has a strong sparsity prior [12]. Thankfully, L1 attention can use softmax as well. .

• (B) Is addressed (also) by the novel attention module, which is designed to allow for direct manipulations of linkages while retaining the transformer approximation of vector-valued edges, which compresses a \(O(d n^2)\) space into \(O(d n)\).

  • This will also allow a relational tagging structure to alleviate the limitations of the finite transformer latent space (i.e. which effects a latent-dimensioned superposition-enhanced array of global variables). ¹²¹² Specifically, transformers instantiate linkages based on correlations in subspaces of the query and key vectors; these linkages have the essential feature that they can forward arbitrary other subspaces of the latent token space. The issue is that this latent token space, while potentially very large (12k dimensions in some LLMs) is still just a vector space, and not a compositional and extensible structure in and of itself (as the whole context across all tokens is). This is likely why you find superposition[13] within latent space. A hypothetical solution is to make a inner-transformer to operate on the latent space of the outer transformer, but this only moves and does not solve the problem!

Solving these two problems will enable the models to operate on data in a new way: rather than the token-policies being permanently and fundamentally tied to the weights of a model, the policies (or programs) exist as a function of the activations & tokens themselves. This is modeled on human cognition: given a verbal description of an algorithm, we can mentally simulate it (if sometimes imperfectly). Current LLMs are limited in these regards; for example, though they know basic set operations and can describe them to you, they typically struggle to apply operations, which are fundamental to mathematics, to new sets [14].

3.3

The third hurdle is training the loop, or ‘boot-up’. This is the largest and most novel challenge. Boot-up entails two elements of complexity: if the memory substrate (the model) implements both continuous high-dimensional vectoral and low-dimensional symbolic functions, then you need to be able to flexibly learn both of those representations. Likewise, general computation can consist of a mix of heuristics (in the form of high-dimensional vector functions) and low-dimensional symbolic functions. This again is mirrored in human cognition: we think with a mix of explicit rules and transformations which are triggered by intuitions (e.g. when solving a mathematical problem), or heuristic guessing triggered by symbolic computation (e.g. guessing the odds of a poker hand after counting & categorizing visible cards).

In a normal transformer, the executable ‘programs’ are stored in the weights; perforce of training on larger and larger datasets, these programs become progressively more general, to the point that they do remarkable things, especially when re-ingesting their own outputs. One shot learning is a form of programming by example – but, again, OOD generalization and level of abstraction is imperfect here: LLMs can reliably fill in examples they have seen, but not directly ‘expand’.

In the proposed model, programs are learned and stored directly in the the tokens & can be accessed and executed directly, and general computation consists of a mix of heuristic and symbolic computation. This entails a number of architectural features / changes:

• (1) The model is trained to exactly implement the symbolic algorithms stored in tokens (not approximate!)

• (2) There must be a mechanism for learning exact and approximate policies for triggering (‘calling’) learned symbolic transformations.

  • In a normal transformer, this is built into the sequence layers/heads, and is chained via backprop; here we chain via both SGD and higher-level symbolic functions.
• (3) The model can translate from heuristic or approximate functions to symbolic functions, and vice-versa

(1) is as motivated above, sec. 3.2; (2) requires critical innovations; (3) is possible if 2 is satisfied.

3.4 Interlude – path-finding

Solving a problem {inducing a model from data, or developing heuristics & algorithms for factorizing and solving CSPs} involves a process analogous to path-finding through a graph of computation and data. At each node in the path, the system must select an operator from those available¹³¹³ Sometimes you must select more than one operator in a sequence; some of these operators may (in true strange-loop fashion) seek to change and transform the path-finding process itself.. Selection requires a policy, search, enumeration, guessing – or a mix of all of these. In systems like DreamCoder [15], policy is handled by sample-efficient ProtoNets to implement heuristics [16] (there are many other algorithms that could serve this purpose, like boosted trees, kernel methods [17], SVM, etc). Critical is sample efficiency: if you need \(k\) samples to learn an approximate strategy at every of \(n\) steps along your path, and each step is distinct, then you need \(\sim k^n\) samples to find your path. If individual steps are related, where each previous step reduces the uncertainty of the following step by (say) 50%, then this is \(\sim k^n 2^{-n}\); if the domain of all paths is finite and can be enumerated, then you can reasonably store them into a heuristic set of policies in a sample-inefficient way.

This is what state-of-the-art models like o3 are doing. Yet we are scientists! We are interested in pushing the frontier of understanding – we want to be able to solve problems that humans have not solved before, problems that do not have an oracle or cannot reasonably discovered through enumeration.

An astute eye again will note that the problem of forming a policy over operator selection is effectively equivalent to the original problem of inducing a model from limited data; this hurdle cannot be avoided through redirection, and must be addressed through a combination of efficient learning algorithms. Fortunately, there are many: in addition to those mentioned in the context of DreamCoder: boosted trees, symbolic manipulation, even diffusion models and other statistically-regularized approaches like GFlowNets [18]. All of these can be decomposed into a composition of symbolic and heuristic functions, hence can be implemented in the proposed system¹⁴¹⁴ One alternative, not explored here, is to have a continuum between low-D and high-D function implementation / approximation, which is interesting but does seem to be the way people think – it’s one or the other. A second alternative is to have only high-dimensional functions; this may very well work, but as it’s the default course, it is well covered by other entities and won’t be explored here..

3.5 Synthesis

The interlude motivates a rough system design:

1. Create a “System 2” which can run symbolic programs to transform tokens, input data, and self-generated traces.

   • The system needs to be vectoral and not an interpreter, like Python or Ocaml, because we need to propagate maintain high-dimensional representations for fitting approximate heuristic functions.

2. Keep a long context of actions and results, just the same as modern transformers.

   • This will require the same set of tricks models use to get long context windows, plus those required to make the new attention performant.
3. Include recurrence in addition to context [19] like the universal transformer [10]¹⁵¹⁵ This is equivalent to unrolling the transformer so that gradients may run backward through time, through the tokens – the discretization step acts as both a clean-up, like DreamerV3 [20]. Other formulations like the implicit function theorem [21] may prove useful.

4. Provide a “System 1” which processes and guesses / intuits in parallel to the symbolic sub-system. Like in people, this is trained “in the background”, based on replay, with SGD.

   • RL systems like EfficientZero [22, 23] indicate that, with sufficient specialization, we can attain near-human sample efficiency here.

5. Add in recursion and frame-switch tokens or meta-cognitive actions for manipulating the memory context.

   • This does not require any architectural changes – only appropriate training, in the same way that LLMs inherit the strange-loopiness of human cognition from natural language.
   • Refer to Figures 1 & 2 for illustrations of variable contexts.

The system thus is a recurrent transformer, trained on symbolic manipulation tasks (e.g. on LEAN or Coq), paired with a background System 1 “intuition generator and compressor” that continually tries to predict internal state¹⁶¹⁶ The System 1 model will start as diffusion transformer, as this is something that we have direct experience with that shows decent compositionality and sample efficiency. While the compositional hypothesis above indicates that System 1 ought to be a combination of low-D and high-D functions, we humans have very limited conscious access to the default intuition-building algorithm. Mirroring this, for now the System 1 model can remain fixed, with higher-level modulation through attention..

3.6 Guessing

When there is an absence of knowledge – when there is no policy – the solver has to guess, whether that’s from random noise (e.g. introduced through random sampling at the last softmax step (as in LLMs), other selection steps, or via the injection of de novo noise into the representation. Those guesses are informed by System 1 and 2¹⁷¹⁷ Forming a potentially long but finite computational path; the axis that yields Turing-completeness still needs to be context length, so that even in the absence of a concrete rule, they can be informed by context and past experience. Guesses then need to be rolled out through the environment and reinforcement, following (for the moment) the current successful playbook of LLMs. As tokens create the computational graph¹⁸¹⁸ An alternative would be to give the model strange-loop access to PyTorch. This seems more efficient, yet more difficult., and can implement algorithms like counterfactual reasoning, this reinforcement is not limited to the sample efficiency of SGD.

4 Closing and ‘strange-ing’ the loop

In our minds, we have both offline, continuous background compression (which forms and updates System 1), but we also have explicit functions that ‘call’ memory formation: surprise, delight, disgust, etc. Only a few of these need be baked into the system; the rest can be learned by making the operation of SGD explicitly callable via a module within the token stream itself. (This is a version of what ‘attention’ means in common parlance: we decide what to attend to and hence understand/predict/remember). As mentioned above, this dissolves some of the distinction between model and optimizer.

A second essential part of strange-loopiness is introspection (“why did this guess work?”; “I can intuit this result – why?”). Humans cannot introspect the state of their synapses (it wouldn’t work out from a numbers perspective!); instead, we derive/compress via input-output example, just the same as we do from interaction with the external world. The system thus must query its own knowledge to transform it, just the same as it induces models from external data. In the poker example given above, this is equivalent to repeatedly asking, with different inputs, “why did I intuit this play for that player?”, which can be passed to a counterfactual reasoning process (or the like). This is a process of taking a set of heuristics and deriving a symbolic rule to supplant or summarize it, as indicated above (3); it’s a path from implicitly learned knowledge to explicit knowledge.

5 Conclusion & summary

An interesting consequence of generalized knowledge being in purely in the tokens is that it means that the base ML model can be smaller and more general – a kernel that’s literally programmed through text. This of course necessitates an explicit index over the knowledge, via the combination of high-D / low -D Systems 1 & 2. Such an index can be iteratively refined through introspection, per above, which facilitates \(O(n \log (n))\) access to knowledge, combating the expensive novel attention computation ¹⁹¹⁹ Another conjecture! Yet this is consistent with the power-law distribution of natural data [24] and providing memory structuring, essential for generalization [25].

There are obviously a lot of holes in this plan for “a pump that pumps information into itself”. Not exclusively:

• Is it possible to build & train a transformer that truly generalizes OOD when executing (nearly) arbitrary algorithms?
• How do you mechanistically “fill in the gaps” when deciding on actions, and open-ended computation is split between low-D and high-D representations?
• How do you prevent catastrophic forgetting when propagating gradients through hybrid computational graphs?²⁰²⁰ Weights needed for executing symbolic programs should not be modified when learning heuristics. Normal ML systems get around this by treating all data as ergodic and IID, and learning over many epochs; fortunately there is plenty of literature describing systems for preventing catastrophic forgetting, e.g. [26].
• Can you resolve many of the problems this approach shares with recurrent neural nets, like exploding / vanishing gradients?
• If the strange loop transformer permits the creation of new computational graphs, how do you augment memory representation & accordingly compositional data structures?

Most of these questions can only be answered by running experiments and trying it out – a loop to make a strange loop. So, onto that!

Timothy Hanson

May 23 2025

Updated July 23 2025 ver. d2755145a1042d2816b158ae5c6b89223f91028d

References