Abstract
This post discusses active learning and reasoning, and the strengths and limitations of using transformers for it. After setting up the problem context, we conclude that for transformers to serve as world-models to these purposes, they will need to adopt a different form that permits multiple optimization steps, and may need changes to improve data efficiency. This is a work-in-progress – we welcome feedback and collaboration!
1 Background
An intriguing problem in machine learning is how to get agents to bootstrap via active learning. If an agent is able to do this, then it can go from \(0 \Rightarrow 1\) (no structure to structured); by induction it can then go from \(1 \Rightarrow N\), where \(N\) is something that humans haven’t done. Human progress is furthered when our tools unlock new capabilities, and so an agent capable of bootstrapping is a worthy goal.
1.1 World model
When an agent (animal, human, AI) interacts with the environment, it can gain valuable knowledge:
- What is possible and likely: \(p(o_t)\) where \(o\) are observations, \(t\) indexes time.11 Spatial indexing is omitted in this post.
- What actions do: \(p(o_{t+1}|a,o_t)\), where \(a\) is an action.
- Valence as to actions and observations: \(p(r|a,o)\) where \(r\) is reward.22 This is of course reinforcement learning (RL), where there is an (approximate) ordering over actions and observations. In RL the agent tries to optimize the (typically time-discounted) reward.
Because interactions are expensive – they consume time and energy – a goal of an agent is make the best use of acquired knowledge when choosing new actions. Typically this is done by building a model of the world, where you approximate \(p(o_{i+1}|a,o_i)\) (Markov state transition function) or \(p(r|a,o)\) (Q-learning) (or some other factorization) with a function approximator, like a neural network. MuZero[1] and EfficientZero[2] are examples of model-based RL; they employ a separate planning module which uses the world model to simulate actions into the future; these actions are selected based on the upper confidence bound (UCB) or upper confidence tree (UCT) to both explore and improve the action selection policy.33 UCB / UCT / PUCT are principled ways of balancing exploration vs exploitation. See Multi-armed bandits with episode context [3].
When used as part of a planner, the goal of the world & reward model is to extrapolate what will happen based on past experience – predict \(p(o_{t+1}, r_{t+1})\) using \(a_t,o_t\). This is very unconstrained – what should the model be?
A common first assumption is consistency – each action produces an expected effect, which is represented by the distribution \(p(o_{t+1}|a,o_i)\). This assumption is not commonly valid in the real world, though: there is unobserved state \(z\), which affects the transition distribution: \(p(o_{t+1}|a,o_t,z_t)\). The world is often consistent if you take into account unobserved variables.44 If you don’t assume consistency, then there is no sense in making a model!
A second assumption, often less explicit, is to assume parsimony: the model should be as simple as possible while explaining the past action & outcomes [4]. Simplicity is hard to quantify, so empirically it is taken to mean that:
- Models are structured hierarchically: sub-modules produce intermediate results, with each submodule contributing small amounts of ‘processing gain’.
- Models have limited dependency graphs: conditional actions depend on a minimum of other variables.
- Models have limited free & non-zero parameters. (This in turn is a different way of saying 2.; you can represent dependency graphs via indicator variables. )
- Models are selected from a space where working solutions are unusually common. 55 Biology leans quite heavily into this – because it is a “blind watchmaker”, it faces no reason to differentiate between searching a space and searching for a search space. Proteins are the canonical example here: it took billions of years and oceans of \(1 \mu m\) organisms to arrive at the central dogma of biology (DNA \(\rightarrow \) mRNA \(\rightarrow \) protein), where the probability of any random protein doing something useful is trillions of times more likely than expected. This is something like meta-structure: the space of structured models is itself structured.
Models in turn can be projected onto the abstract memorization \(\leftrightarrow \) compression axis, where memorization corresponds to little or no computation, and compressed models leverage computation to generate & describe data. Simple models use computation, and so can be considered programs; generating them requires a degree of compression, which is itself intimately related to understanding [5].
Computation is also deeply linked to generalization – if you can run an algorithm to generate existing data, then you can also run it to generate new data (hence the name). Generalization is of obvious importance when exploring an environment.
Deriving models to fit data accurately & parsimoniously ( \( \approx compression\)) is hard! Partly this is because of what Stephen Wolfram dubs the general non-invertability of computation: the most efficient (and often only) way to know what a computation does is to run it. This would imply that looking for models to describe data reduces to search, or at worse to enumeration.
Fortunately, there are working proofs that model search can be efficient: human engineering, biological evolution, neural networks, and the human brain itself. This appears to be the dual of the parsimony criteria: if models are structured hierarchically, with limited dependency graphs, limited free parameters, and from a ’productive’ space, then the search space of possible models is also reduced dramatically – something like \(O(n \log (n))\) or \(O(\log (n \log (n)))…\) where each of the log terms comes from the limits above.66 Because of the reduced dependency graph, it is also possible to do much more local & parallel optimization, a fact that is heavily leveraged in human engineering. (Cutting that dependency graph is, of course, a persistent managerial challenge). Evolution quantifies this more strongly: even with massively parallel search, you absolutely need hierarchically structured systems to make any headway at all!. More succinctly: parsimonious models are easier to search for.
“Perfection is achieved, not when there is nothing more to add, but when there is nothing left to take away.” – Antoine de Saint-Exupéry, Airman’s Odyssey
1.2 Deep learning
Deep learning is a type of model building described above, where instead of action-observation pairs, models serve as function or conditional probability approximators: \(p(y|x)\). Deep learning takes a unique approach to finding models: by relaxing 3. (limited free parameters), deep learning enables stochastic gradient descent (SGD), a rather simple form of search / optimization to readily discover solutions. Overparameterization allows models to work in high-dimensional spaces, which means that (usually) there are no local minima, only saddles, so that all solutions are navigable: you can move from one solution to another with a series of small steps [6]. In deep learning, model weights are typically randomly initialized, and training entails a selection of existing primitives and optimization over them, ala the Lottery ticket hypothesis [7].
By relaxing 3., work in deep learning focuses much on 4. – architectures (’solution spaces’) that empirically create good models, usually by fixing or constraining the dependency graphs 2. The two stand-out examples here are convolutional networks (ConvNets) and Transformers.
Convnets work by ‘baking in’ translational (or other) invariance: the presence of a feature is independent of its location. This is another way of dramatically reducing 2. – instead of an all-to-all matrix multiply, convolution strongly structures computation and dependency; this has the added benefit of reducing the number of parameters 3. By layering convolutional layers with reductions you can compose hierarchical models, satisfying 1.
Transformers have a different ’inductive bias’: they implicitly assume that models (hence computation in the real world) is made up of a series of conditional ‘computational primitives’, where each computational primitive is a composition of vector rotations, scales, and squashing nonlinearity operating in parallel over sets of items called ‘tokens’. The conditions for executing these primitives are gating or ‘attentional’ variables, which are created by pattern matching between tokens.
Transformers assume that these gated computational primitives are natively applied across all positions uniformly – if there is a primitive that say changes the tense of a verb, then by default it changes the tense of all verbs in the input, simultaneously & in parallel. In Transformer parlance: every head is applied equivalently at all positions in a sequence. This is most obvious in an encoder-decoder architecture like BERT [8], but also true in decoder-only models. They thereby assume order invariance, much the same as ConvNets assume translation invariance; adding position encodings allows invariances / equivariances to be learned. Finally, like ConvNets, Transformers are stacked and are hierarchical.
All deep nets assume data is ergodic, or comes from a fixed distribution, equivalent to the consistency assumption – so training involves multiple passes over the data, accumulating errors in the parameters using an exponential moving average. As mentioned above, the parameter space is rendered navigable: if you can move between any model by gradual changes, then the parameters are the only memory you need.
2 Active learning
Active or bootstrapped learning refers to the case that all information related to action selection is derived from interactions with the environment. This is contrary to typical deep learning, where very large datasets are used for training or pre-training, but is common in the RL field, e.g. EfficientZero as mentioned above.77 In practice, of course, it makes full sense to take advantage of human data; for the purposes of going from \(0 \Rightarrow 1\), this is left for future work.
Pre-trained transformers, like GPT-4, are remarkable in that, purely through the process of learning to predict the next word, they learn a compositional and often quite accurate & nuanced model of the world. This suggests that the combination of architecture, training algorithm, and highly structured input data 88 The more structured, the better: Textbooks are all you need [9] can induce a strong world model. Also remarkable that this model can be self-structuring: when applied to itself auto-regressively, it seems to evince ’thinking’ that at least follows the well-worn channels of human thought.
Based on this tremendous emergent representational power, it seems natural to apply transformers to bootstrapped learning problems. DreamCoder [10] was the core inspiration for this; the thought as of \(\sim \) 2 years ago was that, given the power of transformers, it made good sense to use them to store heuristic knowledge instead of the Prototypcial networks [11] that DreamCoder uses. Indeed, like ProtoNets, transformers are well known to show transductive or few-shot learning [12].
2.1 Reasoning, planning, and search
As described above, a goal of an agent is to best use past experience when selecting future actions; compressing experience into a parsimonious world model is a good way of doing this, as it permits generalization via computation. Generalization entails predictions of what actions will do without having to incur the costs of executing them. When coupled to search, this permits planning, exactly as used in model-based RL agents like MuZero.
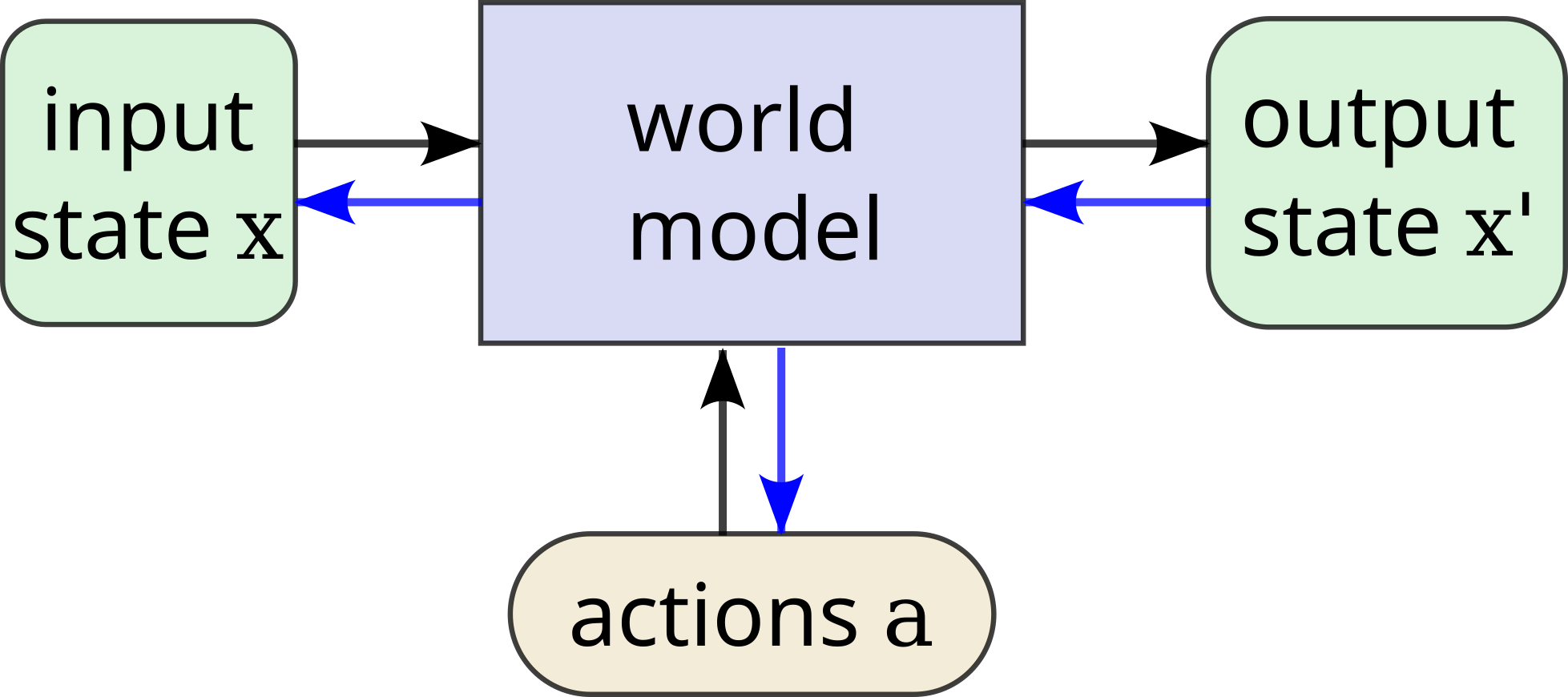
Furthermore, good world models allow both ends-means and means-ends analysis (deduction and induction), wherein end states can be used to optimize actions, actions can be used to optimize end states, and even start states or intermediate states / representations can be optimized; see Figure 199 If you know the full \(p(o_{t+1},r,a,o_t)\) you can condition on any one of those variables. For example, UDRL conditions on \(r\), MCTS planning on \(a\), Q-learning on \(a,r\). But usually you don’t or can’t estimate this full probability.. In a limited sense, this method of passing information via learned models of the world is reasoning. Humans use fuzzy forward- and inverse- models similarly in the process of behavior generation, perception, and problem solving.
Planning equates to selecting an action: \(a’ = \arg \max _a p(r_{t+1}| a, o_t)\) under reward expectation, or \(a’ = \arg \max _{a} f( p(o_{t+1}| a, o_t), g_t)\) where \(g_t\) is a goal, and \(f()\) measures distance to the goal1010 The goal itself can be optimized over, and the distance or matching function \(f()\) to the goal can be learned.. If the environment has unobserved state, action selection requires two optimization steps: perception \(z’ = \arg \max _{z_t} p(o_t | z_t)\) and action \(a’ = \arg \max _{a} p(r_{t+1}| a, o_t, z’)\). Planning may also be ends-means based: \(o_{t-1} = \arg \max _{a_{t-1}} p(o_t, r_t | a_{t-1}, o_{t-1})\) – that is, goal states are selected based on reward, and previous states are selected based on accessibility. As the world is hierarchically structured, action can be hierarchically structured as well: \(g_t = \max _{r_t+1} p(o_{t+1},r_{t+1}| a”, o_t)\)
Human reasoning and planning seems to be a fluid optimization over all free variables – actions, intermediate states, latent variables1111 Inference of latent variables is implict in the case of perception; explicit in the case of e.g. debugging., with possible backtracking, branch-and-bound, or constraint generation to guide that search. The key feature is search – the selection of one from a set of many. Search imbues structure to the sequence of actions; this structure can subsequently be amortized into both a policy and a refined world model, which in turn facilitates better action selection, and therefore is required for bootstrapping and active learning.
More succinctly: you need to do search (or optimization) to bootstrap: go from no structure to some structure.
2.2 Can transformers reason?
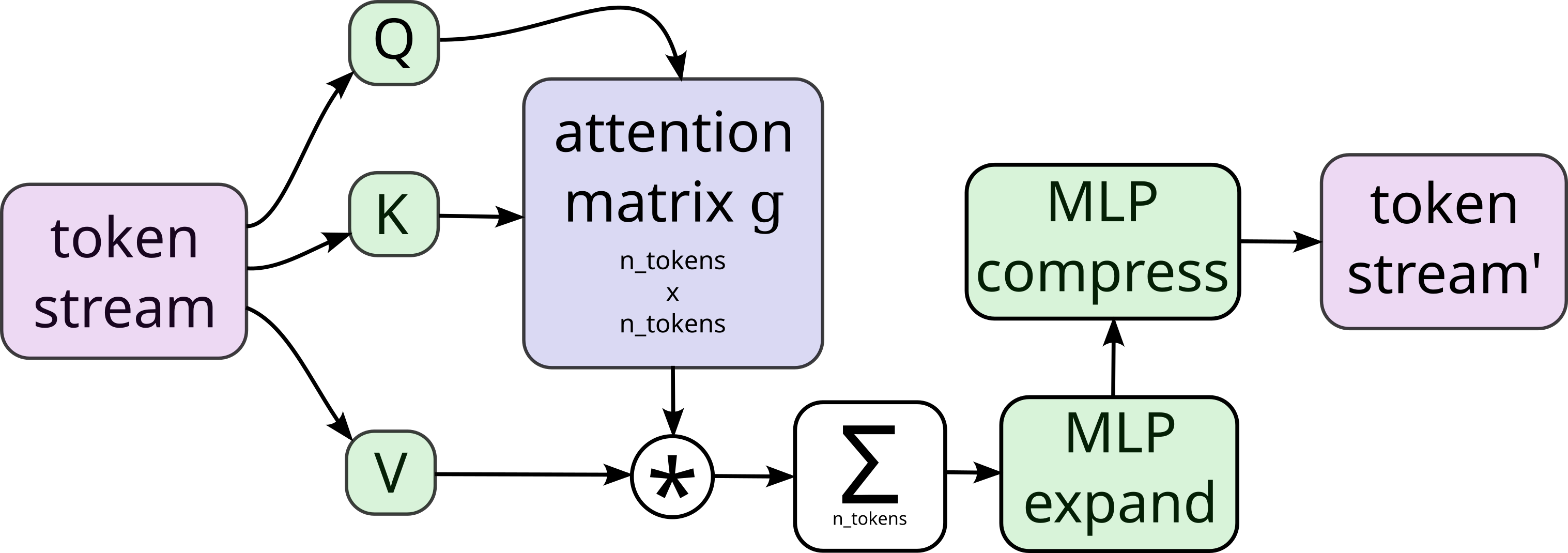
Transformers are a feedforward architecture: they do function approximation, \(y = f(x)\) or \(p(y) \propto p(y|x)\); in a decoder-only transformer, \(y\) is the next token and \(x\) is the context, a list of previous tokens. See Figure 2 for a brief review of one layer / head in a transformer, which is usually tiled tiled horizontally (several heads) and vertically (many layers).
When trained on internet-scale data, Transformers have an unusual emergent property that they seem to form approximate computational models of the world [13] by composing layers of multiple ”induction heads” [14], and can e.g. infer structural priors from spatial data [15, 16]. This compositional, computational modeling of the data, in addition to practical means of training on trillions of tokens [17], leads to foundation models like ChatGPT that are able to learn ”in-context” – that is, respond not only based on their tremendous stored knowledge, but also structure inherent in their immediate input stream or context [12, 18, 19].
This seems like a perfect match for bootstrapped active learning! Computational, compositional models of the world should generalize well, and in-context learning (or transductive learning) means they can be sample efficient, e.g. efficiently use observations.
Yet there are limitations. As transformers are feedforward, the attentional matrix \(g\) is wholly dependent on structure in the input stream, and learning \(\theta \) to drive attention is wholly dependent on conditional structure in the output stream, \(p(y|x)\).
In form of outlined above, reasoning involves propagating information through a world model for argmax optimization. This is impossible in the feedforward one-argument functional form of a transformer. 1212 See also: Large Language Models Still Can’t Plan (A Benchmark for LLMs on Planning and Reasoning about Change) [20]. Policy models are the same functional form, \(a = \pi (\theta ,o)\), hence transformers do learn action-selection policy based on human behavior. In more technical terms:
“Transformers solve compositional tasks by reducing multi-step compositional reasoning into linearized subgraph matching, without necessarily developing systematic problem solving skills.” [21]
However, it is easy to imagine a form that does support reasoning: with decoder-encoder architecture like BERT, you can treat output tokens as \(o_{t+1}, r_{t+1}\) and the input tokens as \(a_t, o_t, z_t\), and perform optimization over \(a_t,z_t\). Per the bootstrapping discussion below, this would require a pre-trained transformer.1313 It may not be efficient, though: in the limit, softmax outputs a categorical variable \(n \choose 1\) which gates per head computation (vector rotation – translation – scaling – squashing). This form of conditional execution is omnipresent in the world, but hard to invert. LLMs of course can and are trained, but they have the advantage that their input has sufficient structure (the incremental, documented nature of human written thought) for generating gating conditions.
Conclusion: Transformers don’t innately reason, but they could with modifications.
2.3 Can transformers bootstrap?
If a transformer is used as a policy model \(a = \pi (\theta ,o)\), then to learn the model parameters \(\theta \) both \(a\) and \(o\) must be structured; yet to structure the search with reasoning or planning, \(\theta \) itself needs to be structured! This results in a Catch-22: transformers cannot be used for bootstrapped learning and reasoning.
This can be (partly) remedied by using a more complete world model, ala EfficientZero [2] and the BERT example above, where the model approximates \(p(o_{t+1}, r_{t+1}| \theta , a, o_{t})\). Then, even under unstructured action selection, \(\theta \) may be optimized just from the observations – though it still cannot generate a policy, since there is no structure in the conditional probability \(p(a | o_t)\).
Again, a way to go from no structure to some structure is with search or optimization: \(a’ = \arg \max _a p(r_{t+1}| a, o_t)\). As there is structure in \(p(o_{t+1},r_{t+1} | a_t, o_t)\) from the forward transition function of the world, reasoning is possible; subsequent training of the full model \(p(o_{t+1}, r_{t+1}, a’, o_{t})\) can induce a policy \(p(a | o_t)\) as well.
Including unobserved variables, you then need three optimization loops: \[ z’ = \arg \max _{z_t} p(o_t | z_t, \theta ) \] \[ a’ = \arg \max _{a} p(r_{t+1}| a, o_t, z’, \theta ) \] \[ \theta ‘ = \arg \max _{\theta } p(o_{t+1}, r_{t+1}, a’, z’, o_t | \theta ) \] Corresponding to perception, reasoning, and model optimization, respectively (and one more in the case of goals!). This makes the algorithm take the form of Expectation Maximization (EM) or coordinate descent. Alternately, it can be considered a factorization along known divisions: world latents \(z\) are independent \(a\), and assumed fast-varying (time factorization) to \(\theta \); \(a\) is quickly varying compared to \(\theta \).1414 LLMs do not distinguish between \(a\) and \(\theta \). Meanwhile, the evolution of cognition seems to entail innovation through factorization: different brain regions handle different (abstract) aspects of the world. Coordinate descent is a common motif used with dependency factorization, per 2. above. Library learning [22, 10, 23, 24] is an important additional optimization loop & factorization not covered here.
To perform these optimizations, a natural choice is the chain rule of calculus, or backprop. You can invert a forward model by deriving gradients and applying e.g. Newton’s method; indeed, SGD does a form of reasoning when repeatedly answering the question: “To improve model performance, which way should I move this weight?”1515 Other approaches like direct feedback alignment [25], or GFlowNets [26] treat learning the inverse as an independent task. In the case of GFlowNets, this seems to provide a good inductive bias for the learning algorithm, speculatively because both forward and reverse model capure modes [27] in the same order, e.g. there is less variance compared to the analytical gradient, ala PPO [28].
That said, SGD has known limits [29], and Survey/Belief Propagation [30] does not readily extend to SAT problems [31] – the first two optimizations are open problems.
Conclusion: Transformers can’t innately bootstrap, but they could with modifications.
2.4 Efficiency
Efficient use of observations is critical for exploring unrestricted spaces; for this reason DreamCoder uses transductive ProtoNets to represent the action-selection policy. Transformers evince the same few-shot learning, but only after training; this training assumes ergodic data, an assumption violated when bootstrapping. Furthermore they typically need at least an order of magnitude more training tokens than parameters to get to the point of few-shot learning.
It is therefore likely, and empirically seems to be the case, that there should be a process of allocation and regularization as a world-model grows in complexity, beyond what is afforded by the ResNet backbone1616 ProtoNets directly support allocation: they store examples.. This has been demonstrated [32], but is not common. Allocation is complementary to the Lottery Ticket hypothesis: instead of eliminating or navigating around randomly-initialized bad hypotheses 1717 Or alternately: culling the dependency graph between variables (both observed and internal), which takes a lot of data., you directly create them.
If reasoning and program synthesis are cast as SAT or SMT problems, then there is clear evidence that NN approaches with SGD are orders of magnitude less efficient than purpose-built solvers like Z3 or Sketch [33]. Sketch uses counterexample guided inductive search – CEGIS – where counterexamples are used to iteratively constrain the solution space [34]. It finds solutions rapidly on problems that SGD struggles with, even with advanced heuristics (restarts, annealing, gradient noise, etc) [29]. This type of local, space-partitioning search is inherently more efficient than global, ergodic optimization when gradients are ill-behaved and should be considered for reasoning agents – e.g. for solving the \(\arg \max \) optimizations above.1818 Also of consideration are orthogonal or second-order approaches – learned policy models that operate over the dependency space. This is partway to providing a ’type system’ to a transformer, or augmenting the form of transformer heads to be \(p(y|(x_a,x_b),(u_a,u_b))\) where \(a\) and \(b\) are type and value. This can be represented by normal transformer heads (if type can be inferred from context) but adding a structural bias could help, like type systems help when programming.
Supposition: Getting transformers to work well as active learners requires something more than SGD.
3 Summary
This post delves lightly into active, model-based, bootstrapped learning. It outlines a mechanistic interpretation of reasoning as a form of information propagation and optimization in a learned model, and from this determined that native transformers can neither reason nor bootstrap. However, appropriate functional and algorithmic modifications should make both of these possible. Work to prove that this is the case is ongoing.
References
[1] J. Schrittwieser, I. Antonoglou, T. Hubert, K. Simonyan, L. Sifre, S. Schmitt, A. Guez, E. Lockhart, D. Hassabis, T. Graepel, T. Lillicrap, and D. Silver, “Mastering Atari, Go, chess and shogi by planning with a learned model,” vol. 588, no. 7839, pp. 604–609. http://www.nature.com/articles/s41586-020-03051-4
[2] W. Ye, S. Liu, T. Kurutach, P. Abbeel, and Y. Gao. Mastering Atari Games with Limited Data. http://arxiv.org/abs/2111.00210
[3] C. D. Rosin, “Multi-armed bandits with episode context,” vol. 61, no. 3, pp. 203–230. http://link.springer.com/10.1007/s10472-011-9258-6
[4] Y. Ma, D. Tsao, and H.-Y. Shum. On the Principles of Parsimony and Self-Consistency for the Emergence of Intelligence. http://arxiv.org/abs/2207.04630
[5] H. Zenil. Compression is Comprehension, and the Unreasonable Effectiveness of Digital Computation in the Natural World. http://arxiv.org/abs/1904.10258
[6] Y. Dauphin, R. Pascanu, C. Gulcehre, K. Cho, S. Ganguli, and Y. Bengio, “Identifying and attacking the saddle point problem in high-dimensional non-convex optimization.” http://arxiv.org/abs/1406.2572
[7] J. Frankle and M. Carbin, “The Lottery Ticket Hypothesis: Finding Sparse, Trainable Neural Networks.” http://arxiv.org/abs/1803.03635
[8] J. Devlin, M.-W. Chang, K. Lee, and K. Toutanova. BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding. http://arxiv.org/abs/1810.04805
[9] S. Gunasekar, Y. Zhang, J. Aneja, C. C. T. Mendes, A. Del Giorno, S. Gopi, M. Javaheripi, P. Kauffmann, O. Saarikivi, A. Salim, S. Shah, H. S. Behl, X. Wang, S. Bubeck, R. Eldan, A. T. Kalai, Y. T. Lee, and Y. Li. Textbooks Are All You Need. http://arxiv.org/abs/2306.11644
[10] K. Ellis, C. Wong, M. Nye, M. Sable-Meyer, L. Cary, L. Morales, L. Hewitt, A. Solar-Lezama, and J. B. Tenenbaum, “DreamCoder: Growing generalizable, interpretable knowledge with wake-sleep Bayesian program learning.” http://arxiv.org/abs/2006.08381
[11] J. Snell, K. Swersky, and R. S. Zemel. Prototypical Networks for Few-shot Learning. http://arxiv.org/abs/1703.05175
[12] T. B. Brown, B. Mann, N. Ryder, M. Subbiah, J. Kaplan, P. Dhariwal, A. Neelakantan, P. Shyam, G. Sastry, A. Askell, S. Agarwal, A. Herbert-Voss, G. Krueger, T. Henighan, R. Child, A. Ramesh, D. M. Ziegler, J. Wu, C. Winter, C. Hesse, M. Chen, E. Sigler, M. Litwin, S. Gray, B. Chess, J. Clark, C. Berner, S. McCandlish, A. Radford, I. Sutskever, and D. Amodei, “Language Models are Few-Shot Learners.” http://arxiv.org/abs/2005.14165
[13] K. Lu, A. Grover, P. Abbeel, and I. Mordatch, “Pretrained Transformers as Universal Computation Engines.” http://arxiv.org/abs/2103.05247
[14] N. Elhage and Anthropic, “A Mathematical Framework for Transformer Circuits,” p. 82. https://transformer-circuits.pub/2021/framework/index.html
[15] R. Rombach, P. Esser, and B. Ommer, “Geometry-Free View Synthesis: Transformers and no 3D Priors,” in 2021 IEEE/CVF International Conference on Computer Vision (ICCV). IEEE, pp. 14 336–14 346. https://ieeexplore.ieee.org/document/9711056/
[16] Y. Chen, F. Viégas, and M. Wattenberg. Beyond Surface Statistics: Scene Representations in a Latent Diffusion Model. http://arxiv.org/abs/2306.05720
[17] J. Hoffmann, S. Borgeaud, A. Mensch, E. Buchatskaya, T. Cai, E. Rutherford, D. d. L. Casas, L. A. Hendricks, J. Welbl, A. Clark, T. Hennigan, E. Noland, K. Millican, B. Damoc, A. Guy, S. Osindero, K. Simonyan, E. Elsen, J. W. Rae, O. Vinyals, and L. Sifre. Training Compute-Optimal Large Language Models. http://arxiv.org/abs/2203.15556
[18] A. Madaan, S. Zhou, U. Alon, Y. Yang, and G. Neubig. Language Models of Code are Few-Shot Commonsense Learners. http://arxiv.org/abs/2210.07128
[19] S. Garg, D. Tsipras, P. Liang, and G. Valiant, “What Can Transformers Learn In-Context? A Case Study of Simple Function Classes.”
[20] K. Valmeekam, A. Olmo, S. Sreedharan, and S. Kambhampati. Large Language Models Still Can’t Plan (A Benchmark for LLMs on Planning and Reasoning about Change). http://arxiv.org/abs/2206.10498
[21] N. Dziri, X. Lu, M. Sclar, X. L. Li, L. Jiang, B. Y. Lin, P. West, C. Bhagavatula, R. L. Bras, J. D. Hwang, S. Sanyal, S. Welleck, X. Ren, A. Ettinger, Z. Harchaoui, and Y. Choi. Faith and Fate: Limits of Transformers on Compositionality. http://arxiv.org/abs/2305.18654
[22] K. Ellis, L. Morales, M. Sablé-Meyer, A. Solar-Lezama, and J. B. Tenenbaum, “Library Learning for Neurally-Guided Bayesian Program Induction.” https://people.csail.mit.edu/asolar/papers/EllisMSST18.pdf
[23] M. Bowers, T. X. Olausson, L. Wong, G. Grand, J. B. Tenenbaum, K. Ellis, and A. Solar-Lezama, “Top-Down Synthesis for Library Learning,” vol. 7, pp. 1182–1213. https://dl.acm.org/doi/10.1145/3571234
[24] G. Grand, L. Wong, M. Bowers, T. X. Olausson, M. Liu, J. B. Tenenbaum, and J. Andreas. LILO: Learning Interpretable Libraries by Compressing and Documenting Code. http://arxiv.org/abs/2310.19791
[25] A. Nøkland. Direct Feedback Alignment Provides Learning in Deep Neural Networks. http://arxiv.org/abs/1609.01596
[26] Y. Bengio, S. Lahlou, T. Deleu, E. J. Hu, M. Tiwari, and E. Bengio. GFlowNet Foundations. http://arxiv.org/abs/2111.09266
[27] J. B. Simon, M. Knutins, L. Ziyin, D. Geisz, A. J. Fetterman, and J. Albrecht. On the Stepwise Nature of Self-Supervised Learning. http://arxiv.org/abs/2303.15438
[28] J. Schulman, F. Wolski, P. Dhariwal, A. Radford, and O. Klimov. Proximal Policy Optimization Algorithms. http://arxiv.org/abs/1707.06347
[29] D. Selsam. The “Terpret Problem” and the limits of SGD. Daniel Selsam. https://dselsam.github.io/the-terpret-problem/
[30] D. E. Knuth and D. E. Knuth, Satisfiablility, printing with corrections ed., ser. The Art of Computer Programming / Donald E. Knuth. Addison-Wesley, no. Volume 4, Fascicle 6.
[31] D. Selsam, M. Lamm, B. Bünz, P. Liang, D. L. Dill, and L. deMoura. Learning a SAT Solver from Single-Bit Supervision. http://arxiv.org/abs/1802.03685
[32] A. Gesmundo and K. Maile. Composable Function-preserving Expansions for Transformer Architectures. http://arxiv.org/abs/2308.06103
[33] A. L. Gaunt, M. Brockschmidt, R. Singh, N. Kushman, P. Kohli, J. Taylor, and D. Tarlow. TerpreT: A Probabilistic Programming Language for Program Induction. http://arxiv.org/abs/1608.04428
[34] A. Solar-Lezama, “Program Synthesis by Sketching.” https://people.csail.mit.edu/asolar/papers/thesis.pdf